In [1]:
import nltk
from nltk.corpus import brown
from collections import Counter
brown_words = brown.words()
unigram_counts = Counter(brown_words)
bigrams = []
for sent in brown.sents():
    bigrams.extend(nltk.bigrams(sent, pad_left=True, pad_right=True))
bigram_counts = Counter(bigrams)

def bigram_LM(sentence_x, smoothing=0.0):
    unique_words = len(unigram_counts.keys()) + 2 # For the None paddings
    x_bigrams = nltk.bigrams(sentence_x, pad_left=True, pad_right=True)
    prob_x = 1.0
    for bg in x_bigrams:
        if bg[0] == None:
            prob_bg = (bigram_counts[bg]+smoothing)/(len(brown.sents())+smoothing*unique_words)
        else:
            prob_bg = (bigram_counts[bg]+smoothing)/(unigram_counts[bg[0]]+smoothing*unique_words)
        prob_x = prob_x *prob_bg
        print(str(bg)+":"+str(prob_bg))
    return prob_x

Language modeling

Another(!) very common problem in NLP:

how likely is that a sequence of words comes from a particular language (e.g. English)?

Odd problem. Applications?

  • speech recognition
  • machine translation
  • grammatical error detection

Language modeling with the perceptron?

Maybe:

  • we have a lot of data: all the English Web
  • we don't have labels
  • can assume everything we see is "good English"; negative instances?
  • we need probabilities; less probable not ungrammatical

Let't think about it differently.

Problem setup

Training data is a (large) set of sentences $\mathbf{x}^m$ with words $x_n$:

\begin{align} D_{train} & = \{\mathbf{x}^1,...,\mathbf{x}^M\} \\ \mathbf{x}& = [x_1,... x_N]\\ \end{align}

for example: \begin{align} \mathbf{x}=&[\text{The}, \text{water}, \text{is}, \text{clear}, \text{.}] \end{align}

We want to learn a model that returns: \begin{align} \text{probability}\; P(\mathbf{x}), \mathbf{for} \; \forall \mathbf{x}\in V^{maxN} \end{align} $V$ is the vocabulary and $V^{maxN}$ all possible sentences

Word counts

Let's take a corpus:

In [2]:
brown.sents()
Out[2]:
[['The', 'Fulton', 'County', 'Grand', 'Jury', 'said', 'Friday', 'an', 'investigation', 'of', "Atlanta's", 'recent', 'primary', 'election', 'produced', '``', 'no', 'evidence', "''", 'that', 'any', 'irregularities', 'took', 'place', '.'], ['The', 'jury', 'further', 'said', 'in', 'term-end', 'presentments', 'that', 'the', 'City', 'Executive', 'Committee', ',', 'which', 'had', 'over-all', 'charge', 'of', 'the', 'election', ',', '``', 'deserves', 'the', 'praise', 'and', 'thanks', 'of', 'the', 'City', 'of', 'Atlanta', "''", 'for', 'the', 'manner', 'in', 'which', 'the', 'election', 'was', 'conducted', '.'], ...]

Count its words and the occurrences of one word:

In [3]:
print(len(brown_words))
print(unigram_counts["the"])

1161192
62713

Word counts to probabilities

probability $P(\text{the}) = \frac{counts(the)}{\sum_{x \in Vocabulary} counts(x)}$

In [5]:
print(unigram_counts["the"]/len(brown_words))

0.05400743374050114

To have a probability distributions and not just scores, the sum of the probabilities for all words must be 1. Let's check:

In [6]:
sum = 0
for word in unigram_counts:
    sum += unigram_counts[word]
print(sum/len(brown_words))

1.0

Unigram language model

Multiply the probability of each word in the sentence $\mathbf{x}$:

$$P(\mathbf{x}) = \prod_{n=1}^N P(x_n) = \prod_{n=1}^N \frac{counts(x_n)}{\sum_{x \in V} counts(x)}$$

Our first language model! What could go wrong?

the most probable word is "the"

  • the most probable single-word sentence is "the"
  • the most probable two-word sentence is "the the"
  • the most probable $N$-word sentence is $N\times $"the"

Sentences with words not seen in the training data have 0 probability.

In [ ]:
print(unigram_counts["genome"]/len(brown_words))

On the way to a better language model

Instead of:

$$P(\mathbf{x}) = \prod_{n=1}^N P(x_n)$$

Let's assume that the choice of a word depends on the one before it:

$$P(\mathbf{x}) = \prod_{n=1}^N P(x_n| x_{n-1})$$

The probability of a word $x_n$ following another $x_{n-1}$ is:

$$P(x_n| x_{n-1})=\frac{bigram\_counts(x_{n-1}, x_n)}{counts(x_{n-1})}$$

This is the bigram language model.

Bigram language model in action

$$\mathbf{x}=[\text{The}, \text{water}, \text{is}, \text{clear}, \text{.}]$$\begin{align} P(\mathbf{x}) =& P(\text{The}|\text{None})\times P(\text{water}|\text{The})\times P\text{is}|\text{water})\times\\ &P(\text{clear}|\text{is})\times P(\text{.}|\text{clear})\times P\text{.}|\text{None}) \end{align}
In [7]:
x = ["The", "water", "is", "clear", "."]
print(bigram_LM(x))

(None, 'The'):0.11412626438786187
('The', 'water'):0.0009644530173601543
('water', 'is'):0.030162412993039442
('is', 'clear'):0.002497253021676156
('clear', '.'):0.091324200913242
('.', None):1.0
7.571487129955549e-10

Longer contexts

$$P(x|context) = \frac{P(context,x)}{P(context)} = \frac{counts(context,x)}{counts(context)} $$

In bigram LM $context$ is $x_{n-1}$, trigram $x_{n-2}, x_{n-1}$, etc.

The longer the context:

  • the more likely to capture long-range dependencies: "I saw a tiger that was really very..." fierce or talkative?
  • the sparser the counts (zero probabilities)

5-grams and training sets with billions of tokens are common.

What about the unseen words?

<img style:"float:left" src="images/Fairbanks_Robin_Hood_standing_by_wall_w_sword.jpg" />

... stealing from the rich and giving to the poor!

By United Artists, cinematographers Arthur Edeson & Charles Richardson - Here, Public Domain, Link

Smoothing intuition

Taking from the frequent and giving to the rare (discounting)

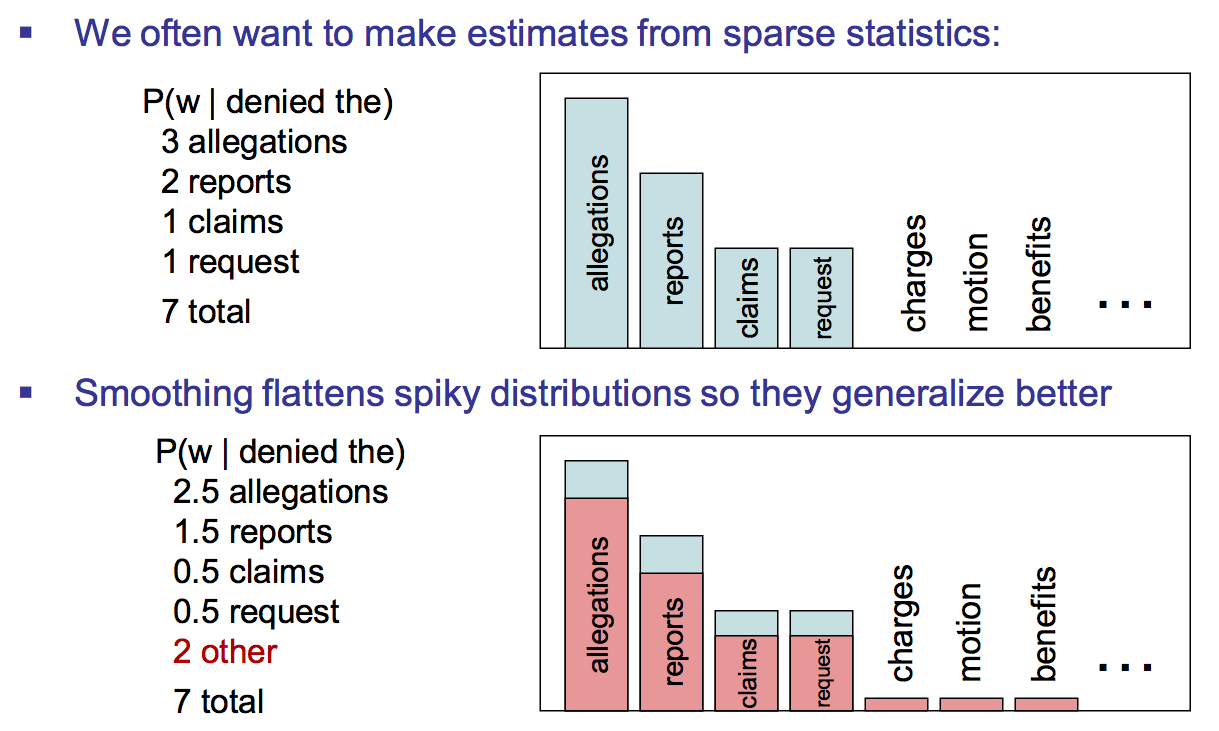
Smoothing

Pretend we have seen everything at least once:

$$P_{add-1}(x_n|x_{n-1}) = \frac{counts(x_{n-1},x_n)+1}{counts(x_{n-1}) + |V|} $$

Add-1 puts too much probability mass to unseen bigrams, better to add-$k, k<1$: $$P_{add-k}(x_n|x_{n-1}) = \frac{counts(x_{n-1},x_{n})+k}{counts(x_{n-1}) + k|V|} $$

Smoothing in action

In [10]:
x = ["The", "water", "is","crystal", "clear", "."]
print(bigram_LM(x))

(None, 'The'):0.11412626438786187
('The', 'water'):0.0009644530173601543
('water', 'is'):0.030162412993039442
('is', 'crystal'):0.0
('crystal', 'clear'):0.0
('clear', '.'):0.091324200913242
('.', None):1.0
0.0
In [11]:
print(bigram_LM(x, smoothing=1.0))

(None, 'The'):0.05771655834707537
('The', 'water'):0.00012634837405436138
('water', 'is'):0.00024783147459727387
('is', 'crystal'):1.5135462388375965e-05
('crystal', 'clear'):1.7832941008631143e-05
('clear', '.'):0.0003731475887558193
('.', None):0.4681656467909492
8.521683357303412e-23

More smoothing

If a word was never encountered in training, any sentence containing will have probability 0

It happens:

  • all corpora are finite
  • new words emerging

Common solutions:

  • Generate unknown words in the training data by replacing low-frequency words with a special UNKNOWN word to represent them
  • Use classes of unknown words, e.g. names and numbers

Evaluation

Intrinsic evaluation for language modeling

How well does our model predict the next word?

I always order pizza with cheese and...

  • mushrooms?
  • bread?
  • and?

Measure accuracy/perplexity (how surprised is the LM by the correct word)

Evaluation

Extrinsic evaluation for language modeling

  • Grammatical error correction: detecting "odd" sentences and propose alternatives
  • Natural lanuage generation: prefer more "natural" sentences
  • Machine translation, speech recognition