More language modeling¶
<img style:"float:left; width=75%" src="images/dinosaur_ngrams.png"/>
Recap by the Berkeley NLP group
Simple Linear Interpolation¶
Let's combine them (for 3gram LM, $k=2$):
\begin{align} P_{SLI}(x_n|x_{n-1},x_{n-2})& = \lambda_1 P(x_n|x_{n-1},x_{n-2})\\ & + \lambda_2 P(x_n|x_{n-1})\\ & + \lambda_{k+1}P(x_n) \qquad \lambda_i>0, \sum \lambda_i = 1 \end{align}Every model can be fooled, avoid relying on any one exclusively!
Syntax-based language models¶
<img style:"float:left" src="images/depLM.png"/>
$$P(\text{binoculars}|\text{saw})$$more informative than:
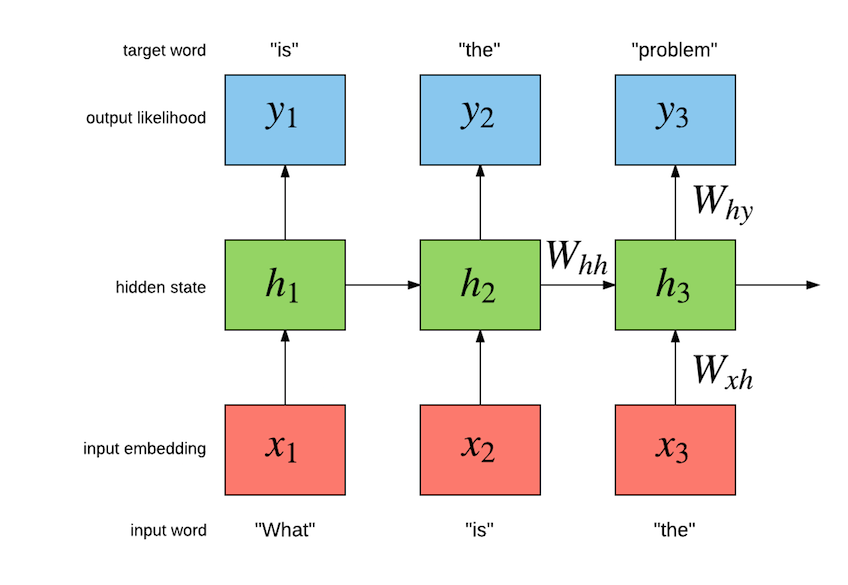
$$(\text{binoculars}| \text{strong}, \text{very}, \text{with}, \text{ship}, \text{the},\text{saw})$$Neural language models¶
Words and contexts are represented by sets of numbers (vectors):
- similar word/phrases have similar representations
- unseen word combinations have non-zero probability
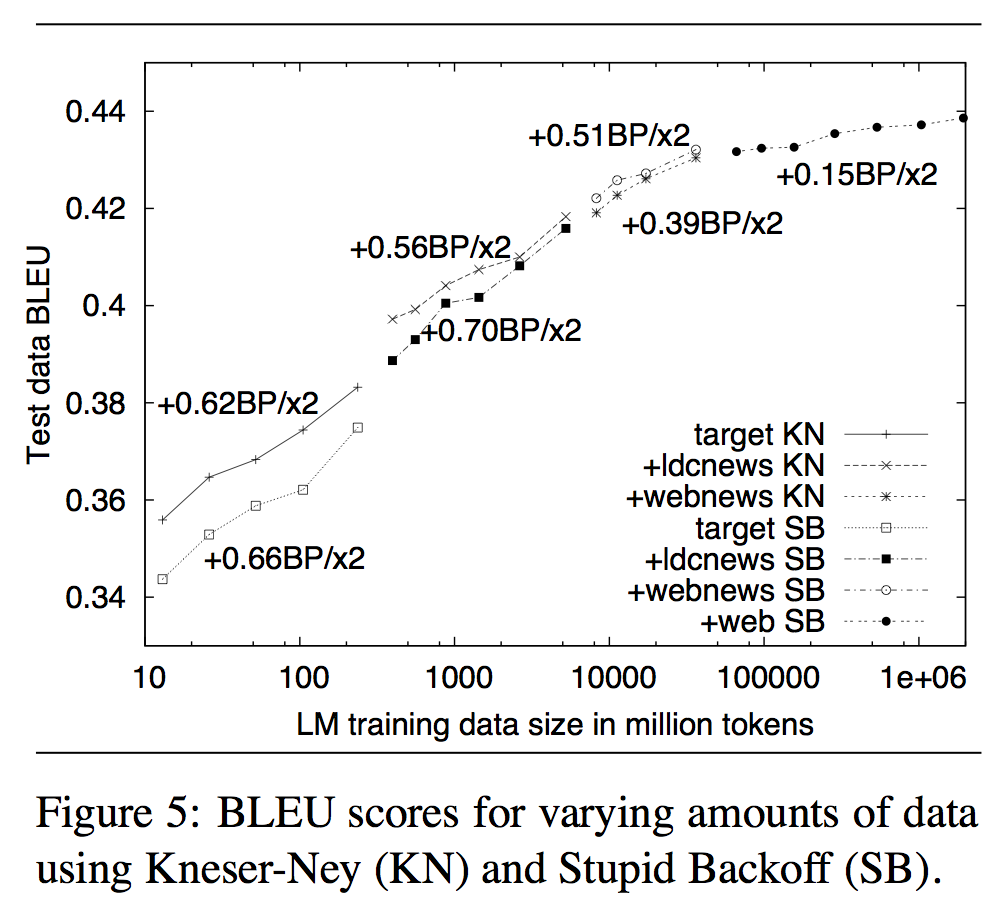
Last words: More data defeats smarter model!¶
Last words (really!)¶
Recap:
- language models capture a simplified notion of language
- context matters (use bigrams or more)
- very active research topic with many applications