import re
from collections import Counter
# For the example later
example_text = open("review_polarity/txt_sentoken/pos/cv750_10180.txt").read()
bag_of_words=Counter({'and': 37, 'is': 26, 'he': 11, 'great': 10, 'carlito': 9, 'film': 8, 'but': 8, 'some': 7, 'pacino': 7, "carlito's": 7, 'palma': 5, 'well': 5, 'like': 5, 'woman': 4, 'amazing': 4})
Text classification
A very common problem in NLP:
Given a piece of text, assign a label from a predefined set
What could the labels be?
- positive vs negative (e.g. sentiment in reviews)
- about world politics or not
- author name (author identification)
- pass or fail in essay grading
In this section¶
We will see how to:
- representing text with numbers
- learn a classifier using the perceptron rule
... and you will ask me questions!
The maths we need is addition, subtraction, multiplication and division!
Sentiment analysis on film reviews¶
Representing text with numbers¶
print(example_text)
Counting words¶
dictionary = Counter(re.sub("[^\w']"," ",example_text).split())
print(dictionary)
Bag of words representation¶
- The higher the counts for a word, the more important it is for the document
- No document has every word; most have 0 counts (implicitly)
Anything missing?
- which words to keep?
- how to value their presence/absence?
- word order is ignored, could we add bigrams?
Choice of representation (features) matters a lot!
Our first classifier¶
Now we have represented a text as counts over words/features.
We need a model to decide whether the review is positive or negative.
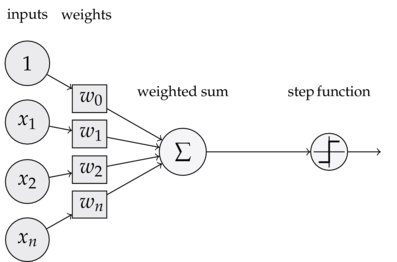
If each word $n$ has counts $x_n$ in the review and is associated with a weight ($w_n$), then:
$$\hat y = sign(\sum_{n=1}^N w_nx_n) = sign(\mathbf{w} \cdot \mathbf{x})$$print(bag_of_words)
weights = dict({'and': 0.0, 'is': 0.0, 'he': 0.0, 'great': 0.0,\
'carlito': 0.0, 'but': 0.0, 'film': 0.0, 'some': 0.0,\
'carlito\'s': 0.0, 'pacino': 0.0, 'like': 0.0,\
'palma': 0.0, 'well': 0.0, 'amazing': 0.0, 'woman': 0.0})
score = 0.0
for word, counts in bag_of_words.items():
score += counts * weights[word]
print(score)
print("positive") if score >= 0.0 else print("negative")
The perceptron

Proposed by Rosenblatt in 1958 and still in use by researchers
Supervised learning¶
Given training documents with the correct labels
$$D_{train} = \{\mathbf{x}^1,y^1)...(\mathbf{x}^M,y^M)\}$$Find the weights $\mathbf{w}$ for the linear classifier
$$\hat y = sign(\sum_{n=1}^N w_nx_n) = sign(\mathbf{w} \cdot \mathbf{x})$$so that we can predict the labels of unseen documents
Supervised learning¶
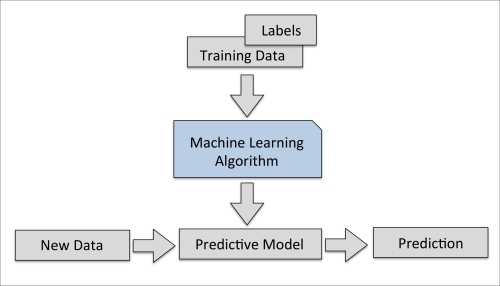
Learning with the perceptron
\begin{align} & \textbf{Input:} \; D_{train} = \{(\mathbf{x}^1,y^1)...(\mathbf{x}^M,y^M)\}\\ & set\; \mathbf{w} = \mathbf{0} \\ & \mathbf{for} \; (\mathbf{x},y) \in D_{train} \; \mathbf{do}\\ & \quad predict \; \hat y = sign(\mathbf{w}\cdot \phi(\mathbf{x}))\\ & \quad \mathbf{if} \; \hat y \neq y \; \mathbf{then}\\ & \quad \quad \mathbf{if} \; \hat y\; \mathbf{is}\; 1 \; \mathbf{then}\\ & \quad \quad \quad update \; \mathbf{w} = \mathbf{w} - \phi(\mathbf{x})\\ & \quad \quad \mathbf{else}\\ & \quad \quad \quad update \; \mathbf{w} = \mathbf{w} + \phi(\mathbf{x})\\ & \mathbf{return} \; \mathbf{w} \end{align}
- error-driven, online learning
- $x$ is the document $\phi(x)$ is the bag of words, bigrams, etc.
A little test¶
Given the following tweets labeled with sentiment:
| Label | Tweet |
|---|---|
| negative | Very sad about Iran. |
| negative | No Sat off...Need to work 6 days a week. |
| negative | I’m a sad panda today. |
| positive | such a beautiful satisfying day of bargain shopping. loves it. |
| positive | who else is in a happy mood?? |
| positive | actually quite happy today. |
What features would the perceptron find indicative of positive/negative class?
Would they generalize to unseen test data?
Sparsity and the bias¶
In NLP, no matter how large our training dataset, we will never see (enough of) all the words/features.
- features unseen in training are ignored in testing
- there are ways to ameliorate this issue (e.g. word clusters), but it never goes away
- there will be texts containing only unseen words
Bias: that appears in each instance
- its value is hardcoded to 1
- that 1 in the diagram
- effectively learns to predict the majority class
Evaluation¶
The standard way to evaluate our classifier is:
$$ Accuracy = \frac{correctLabels}{allInstances}$$What could go wrong?
When one class is much more common than the other, predicting it always gives high accuracy.
Evaluation¶
| Predicted/Correct | MinorityClass | MajorityClass |
|---|---|---|
| MinorityClass | TruePositive | FalsePositive |
| MajorityClass | FalseNegative | TrueNegative |
Time for (another!) test¶
Discuss in pairs what features you would use in a classifier that predicts FAIL/PASS for an essay!